Letters From a Black Hole

Case Studies

Some of the Black Holers and Big Bangers involved

1. Prof. G.W. Bruhn (who has adopted the email alias, Ernest S. Gullible)
2. Prof. G. 't Hooft
3. Prof. M.H.A. MacCallum
4. Prof. A. Krasinski
5. Prof. R.P. Kerr
7. Prof. F. W. Hehl (Gravitation and Relativity Group, University of Cologne)
8. Prof. Edwin F. Taylor and Prof. Edmund Bertschinger (a dynamic duo at MIT)
9. The ignoble Editorial Board of the International Journal of Theoretical Physics - a particularly revealing example of the organised methods of suppression and scientific fraud used by the black holers and big bangers.

Preamble

According to the theory of black holes, the black hole has and does not have an escape speed simultaneously at the 'event horizon' (see here). That this is impossible is sufficient to invalidate black hole theory without a single equation.

According to the theory of black holes the finite mass of a black hole is concentrated at its 'physical singularity, where volume is zero, density is infinite, and spacetime is infinitely curved. There are forces in General Relativity, but gravity is not one of them, because it is 'spacetime curvature' (see here). Thus, infinite spacetime curvature = infinite gravity. However, no finite mass has zero volume infinite density, and infinite gravity, anywhere.

The usual line-element for Minkowski space, in spherical coordinates, is (using c = 1),

The so-called "Schwarzschild solution" is not Schwarzschild's solution. It is in fact a corruption of the Schwarzschild and Droste solutions, due to David Hilbert. Here is Hilbert's solution:

wherein m is allegedly the mass of the source of an associated gravitational field, the quantity r is the 'radius', so that there are two purported "singularities", one at r = 2m and another at r = 0. It is routinely asserted that r = 2m is a 'coordinate' or 'removeable' singularity which denotes an 'event horizon', at the so-called 'Schwarzschild radius', and that the 'true' or 'physical' or 'curvature' singularity is at r = 0. But here is the actual solution obtained by Karl Schwarzschild, in 1915 (published 1916):

wherein α is an undetermined positive real constant. Note that Schwarzschild's actual solution is singular only at r = 0; in other words, Schwarzschild's actual solution is undefined at m = 0 owing to division by zero. Contrary to the claims of cosmologists, Schwarzschild did not set α = 2m, where m is the mass of the source of the gravitational field; he did not breathe a single word about the object that has come to be called a black hole; he did not derive the so-called 'Schwarzschild radius' attributed to him; he did not claim that there is an 'event horizon'; and his solution clearly forbids the black hole because when Schwarzschild's r = 0, his R = α, and there is no possibility for his R to be less than α, let alone take the value R = 0. All this can be easily verified by simply reading Schwarzschild's original paper. Thus, eq. (2) down to r = 0 therein is inconsistent with Schwarzschild's actual solution eq. (3). When presented with Schwarzschild's real solution, Bruhn (see his communications below) told me "Whatever Schwarzschild did is not relevant". 't Hooft even lied about it (as his communication below attests).

Here is Droste's solution, obtained by him independently of Schwarzschild, in May 1916, by a different method:

Note that eq. (4) is singular only at r = α and that it is entirely consistent with Schwarzschild's actual solution, eq. (3). In addition, Droste anticipated the erroneous procedure that conjures up the alleged black hole (driving r down to zero in eqs. (2) and (4)), noting that such a procedure leads to a non-static solution to a static problem, and is therefore false.

Finally, here is the general solution I have obtained (amongst other things):

wherein both r_o and n are entirely abritrary constants and the quantity 1/C(r) is the Gaussian curvature of any spherically symmetric geodesic surface in the spatial section of the manifold, from which R_c(r) is the radius of Gaussian curvature by the formality of it being the inverse square root of the Gaussian curvature (and does not directly determine any distance in the gravitational manifold, let alone the geodesic radial distance from the arbitrary point at the centre of spherical symmetry). Eq. (5) yields an infinity of equivalent line-elements. Setting r_o = 0, n = 3 and r non-negative gives Schwarzschild's actual solution. Setting r<_o = α, n = 1 and r non-negative (which actually implies, by the geodesic radius, that r ≥ α), yields Droste's solution. Taking r_o = 0, n = 1 and r< non-negative, yields Brillouin's solution (1923). Eq. (5) is well-defined for all r< ≠ r<_o and it is singular only at one point; at the arbitrary parametric point r<_o. Note also that in expressions (3), (4) and (5), all the components of the metric tensor are modified by the presence of the constant α. However, according to the cosmologists, in relation to expression (2), only g₀₀ and g₁₁ are modified by the presence of their term 2m. The black holers think that their term r<² in expression (2) is completely unaffected by the geometry of Einstein's gravitational field (i.e. that r in expression (2) is not directly affected by their term 2m therein). Since in eq. (2), g₂₂ = -r² and g₃₃ = -r²sin²θ, the cosmologists therefore claim that neither g₂₂ nor g₃₃ are affected by their term 2m; that these two components of the metric tensor are independent of the alleged presence of matter denoted by their term 2m. This is incorrect, as expressions (3), (4) and (5) clearly reveal. So the black holers modify the components of the metric tensor selectively, in violation of the rules of geometry.

The Letters From a Black Hole

I reproduce Bruhn's communications here, in full, so that the possibility of his alteration of documents without detection is obviated (he has a track record of being rather careless with the truth). 't Hooft's communication is here (as he too has demonstrated a blatant disregard for the truth). Bruhn has posted to his website an exposition in which he ridicules me and my work. There are actually two versions of his exposition to date. Both versions are included in the Bruhn communications I have posted herein. In the second version Bruhn introduces the Eddington-Finkelstein 'coordinates' oblivious to that fact that it makes no difference whatsoever to the invalidity of the black hole. I have dealt with the Eddington-Finkelstein 'coordinates' in this paper and the "isotropic coordinates" in this paper. Evidently Bruhn has not read these papers either, or understood nothing if he did read them.

Now according to Bruhn, the quantity r appearing in eq. (2) is "the radius of a 2-sphere". According to 't Hooft it is "a gauge choice: it defines the coordinate r". It is also called variously, by the black holers (see any of their books and papers), merely using vague jargon and assorted gobbledygook, the "radius of a sphere", the "areal radius", the "reduced circumference", the "coordinate radius", the "radial coordinate", the "radial space coordinate". In relation to eq. (2) they call the particular case r = 2m the 'Schwarzschild radius' or the 'gravitational radius', which they also assert is related to a kind of black hole in Newton's theory (wherein r is actually a radial distance from the centre of mass at the centre of spherical symmetry, and identical to the inverse square root of the Gaussian curvature of any spherically symmetric surface in the space, owing to the Euclidean structure of Newton's space). Cosmologists routinely claim that the purely theoretical Michell-Laplace Dark Body is a kind of black hole, which is demonstrably false. Indeed, there is no 'gravitational collapse' associated with the Michell-Laplace Dark Body, no infinitely dense point-mass singularity, no event-horizon, it has an escape speed whereas the black hole actually has no escape speed, and there is always a class of observers that can see it whereas there is no class of observers that can see the alleged black hole. Returning from this digression, no cosmologist has ever correctly identified the quantity r in eq. (2). It is, as I have maintained in all my relevant publications and correspondence, the inverse square root of the Gaussian curvature of the spherically symmetric geodesic surface in the spatial section of the metric. In other words, at any point in the metric space described by eq. (2) (correctly however by Droste's solution eq. (4)), the quantity r therein determines the Gaussian curvature of the spherically symmetric geodesic surface in the spatial section, containing the point. It is neither radius nor distance, it is not the radius of a 2-sphere', not a 'gauge choice' that 'defines the coordinate r'. The quantity R_c(r) given in eq. (5) is the inverse square root of Gaussian curvature of the associated spherically symmetric geodesic surface. The radial distance is given by the integral of the square root of the negative of the component of the metric tensor containing the square of the differential element of the inverse square root of Gaussian curvature (see below for the mathematical expression). Repeated requests to Bruhn, 't Hooft, MacCallum, and Krasinski, amongst others, to prove that r in their eq. (2) is the radius have been met with silence.

When confronted with my simple proof of the falsity of his claim that in eq. (2) the quantity r is the 'radius of a 2-sphere', Bruhn admitted that his claim is false; he said "OK so far. I think here we have arrived at an important point to think over again" (see his communications), and up to that time he was ignorant of the relevant elementary differential geometry. However, notwithstanding this admission, he has made no note of it in his articles or otherwise on his website. In fact, he has not posted to his website any of my replies to him, thereby suppressing the proofs of the falsity of his claims (he who, quite clearly disingenuously, contacted me and invited me to 'discussion'). When confronted with the proof of the falsity of his "gauge choice" nonsense, 't Hooft did not understand it and so did not take account of it, just ignored it. On his website, 't Hooft calls me Mr. C and although he now admits there that I am right, he vilifies me nonetheless, along with Mr. E (Professor Myron Evans), Mr. L (Dr. Chung Lo), Mr. DC (Dimi Chakalov), and Mr. L (Professor Angelo Loinger).

Now the proof that r in eq. (2) in fact determines the Gaussian curvature rather than a distance in the manifold, is sufficient to completely invalidate all the claims for black holes. Bruhn's admission of the falsity of his oft repeated claims that r in eq. (2) is the "radius of a 2-sphere", and his admission of the validity of my proof that it is indeed the inverse square root of the Gaussian curvature, amounts to an admission that all the claims about black holes made cosmologists are false. In an attempt to save face, Bruhn entered into a long and trivial diatribe on irrelevant issues and misconceptions, ignored the facts, conjured up fantasies and falsely attributed his constructions to me (see his communications). 't Hooft repeatedly failed to offer the requested proof that r in eq. (2) is the radius. Both Bruhn and 't Hooft merely reasserted, without any proof whatsoever, that 0 ≤ r in eq. (2).

Here is a simple proof that r in eq. (2) determines the Gaussian curvature. The line-element, in spherical coordinates, for 3-dimensional Euclidean space is,

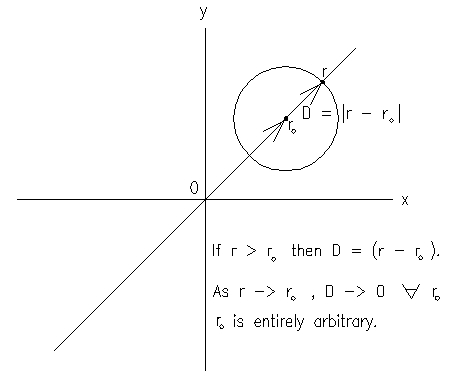
The significance of the parameter r in eq. (5), and hence in eq. (2), is now apparent:- it is the quantity r in Minkowski space as described by eq. (1) above, so that Minkowski space is a parametric space for Einstein's gravitational field, by which distances between two collinear points in Minkowski space are mapped into both the Gaussian curvature and the proper radius of the supposed gravitational field. Thus, consider the distance D between any two arbitrary points in Minkowski space, one of which is at some arbitrary fixed point in Minkowski space at a distance r_o ≥ 0 from r = 0 in Minkowski space as described by eq. (1) above. What is the corresponding distance in the gravitational manifold? The answer is given by the mapping (eq. (13)) into the proper radius R_p of the gravitational manifold, and associated with it is the Gaussian curvature (also obtained by a mapping; by eq. (5)) at any point at that proper radius in the gravitational manifold, and the radius of Gaussian curvature is not the same as the proper radius in the gravitational manifold. This is all due to the non-Euclidean structure of Einstein's gravitational field. In the case of eq. (2), the inverse square root of the Gaussian curvature takes on the same values as the parameter r, owing to the choice of r_o, as amplified by eq. (5), but the reckoning of the parametric distance D between some moving point r and the arbitrary fixed point r_o, both on a single radial line though r = 0 of Minkowski space, is from the point at the distance r_o = α from r = 0 in Minkowski space. All that is mapped is the distance D between two arbitrary points, one of which is fixed, but this distance can be given explicitly in terms of the parametric r and r_o in the mappings, as eq. (5) shows, without loss of generality, by keeping collinear the radial lines from r = 0 in Minkowski space to r and to r_o ≠ 0 respectively, since any radius vector of length D from some point at a distance r_o from r = 0 in Minkowski space traces out the surface of a sphere of radius D centred at the point r_o. To retain the scalars r and r_o one need only consider the distance D along the single radial line through r and r_o and r = 0 in Minkowski space. It is seen from eqs. (5) and (13) that for the case of eq. (2), the choice of r_o = α, r non-negative, causes the α terms to drop out of the expression for the inverse square root of the Gaussian curvature associated with the gravitational manifold, but that does not change the parametric location of the point at the centre of spherical symmetry in Minkowski space: it is still fixed at the point r_o = α, according to the solution obtained by Droste, and, as r approaches r_o = α from above, the distance D between them approaches zero and the corresponding proper radius in the gravitational manifold also approaches zero and the Gaussian curvature approaches 1/α² (so that the inverse square root of the Gaussian curvature approaches α). Thus one could replace |r - r_o| in eq. (5) with the distance D between any two arbitrary points in Minkowski space and just consider what happens to the corresponding proper radius and Gaussian curvature in the gravitational field as the parametric distance D approaches zero. However, I retained the scalars r and r_o in all my work to illuminate their parametric nature in mappings, so that the role of the quantity r in the solutions obtained by Schwarzschild, Droste, Brillouin, and in Hilbert's corruption, is amplified. In his attempts to refute me Bruhn failed to realise that the radial distance D is fixed for a given sphere centred at an abitrary point r_o despite his introduction of vectors r and r_o and it is essentially this distance D, a scalar, which is mapped into Schwarzschild spacetime. As remarked above, Bruhn's insistence on vector representation in relation to my work, propounded in his aforementioned papers, is unnecessary, and his counter arguments totally irrelevant, since one can just replace |r - r_o| in eq. (5) above with the distance D between any two points in Minkowski space, irrespective of the locations of the said two points (i.e. not necessarily on the same radial line through r = 0), as I pointed out to him repeatedly by the fact that in Euclidean space a sphere of fixed radius D, centred at the extremity of an arbitrary fixed vector r_o, can be described by the vector equation (r - r_o)∙(r - r_o) = D² = |r - r_o|², but which he would not acknowledge, and instead falsely accused me of claiming that |r - r_o| = |r - r_o| always and then made a great song and dance about it nothwithstanding that the latter assertion was concocted by Bruhn himself, along with a host of other rot which he falsely attributed to me, as his communications reveal. His inventions appear nowhere in my works. Thus Bruhn attempted to falsify my work with his own impositions, avoided the core issues, and went off on long, irrelevant and erroneous tangents of his own construction, by which he attempted to discredit my work, and still had the gall to repeatedly call me a "pseudo-scientist" despite his own admissions as to his poor knowledge of differential geometry. The figure below illustrates the simple geometry in parametric Minkowski space (with the 3^rd dimension suppressed). Note that if the radial line shown is the directed real line then positive and negative values of r and r_o are permitted, since only parametric distance is mapped, into a distance (a scalar) and into a Gaussian curvature (a scalar) in the gravitational manifold, and this is precisely the content of eqs. (5) and (13) above. It is also clear from the figure that if r_o = 0 then the parametric distance is just D = r = |r|, and again the vector notion is superfluous, since distance is a scalar. It is also easily seen from the figure, rather trivially, that the parametric distance D can be given in terms of parametric vectors r and r_o so that the radius of the resulting sphere is D = |r - r_o|, which is not the same as |r - r_o| in general. But that is of no consequence because D is fixed for the said sphere and D is what is mapped, and the point at the extremity of the vector r can approach the point at the extremity of the vector r_o along any radial line (r - r_o) (or indeed along any other curve) because all that is mapped is the distance D = |r - r_o| between the points at the extremities of the two vectors as r → r_o (thus, D → 0). However, in order to retain the scalars r and r_o explicitly, as they appear in the line-elments obtained by Schwarzschild, Droste, Brillouin, Hilbert's corruption, and others, I strictly apply the configuration depicted in the figure, without any real loss of generality, for my eq. (5), since the vectors r and r_o can always be brought into collinearity, in which case the distance D = |r - r_o| = |r - r_o| and it does not matter if r is greater than or less than or equal to r_o and the point r then approaches the point r_o along a radial line (the directed real line depicted), and the distance to the fixed point r_o is entirely arbitrary. All of this is elementary mathematics, yet Bruhn did not grasp it, and it is evidently beyond the ken of Messrs. 't Hooft, M.H.A. MacCallum, A Krasinski, Roy P. Kerr, and the whole bevy of cosmologists listed here.

The simple geometry in parametric Minkowsi space.

In view of the foregoing, eq. (1) can be generalised thus

= dt2 - (r - ro)2 |r - ro|2 dr2 - |r - ro|2(dθ2 + sin2θ dφ2)

where D = |r - r_o| is just the distance between the spherical surfaces of the spheres of radii r and r_o respectively (i.e. the distance between two points on a common radial line passing through r = 0, located at the distances r and r_o respectively from the origin of the coordinate system at r = 0, as depicted in the figure above). Negative values of r and r_o are permitted by virtue of the fact that the said radial line is really nothing other than the directed real line (although the negative values are really redundant since they add nothing to the overall results, since distance is the real issue, but I included them for mathematical completeness). Note that in the case of r_o = 0, r ≥ 0, eq. (1b) reduces to eq. (1). Moreover, substituting D = |r - r_o| into eq. (1b) gives

which is precisely eq. (1) except for the triviality of notation.

Calculating the proper radius for eq. (1b) gives,

where B is a constant of integration. Now for R_p(r_o) = 0, it follows that B = 0, and so R_p(r) = |r - r_o|, and so in eq. (1c), R_p(D) = D, where D is the inverse square root of the Gaussian curvature; then for eq. (1c) R_p(D=0) = 0.

The cosmologists also make a great fuss over geodesic completeness. Well, in relation to their eq. (2) above, Hagihara proved in 1931 that all geodesics that do not run into the boundary at r = 2m are geodesically complete. This is not surprising since K = 1/4m² is simply the value of the Gaussian curvature at the very point R_p(2m) = 0 at the centre of spherical symmetry of the spacetime described by eq.(2).

The cosmologists make much fanfare of an infinitely dense 'point-mass singularity' at the heart of their black hole, produced, they say, by irresistible gravitational collapse, surrounded by an 'event horizon'. Yet according to Special Relativity, infinite densities are forbidden because that would require infinite energy, or equivalently that a material object can travel at the speed of light in vacuo, contrary to Einstein's tenets. This is easily seen as follows. Consider a cuboid rest-mass m_o of sides length L_o oriented along each orthogonal Cartesian axis. Let it move with constant rectilinear velocity v in the x-direction, relative to an observer of rest-masss M_o. By Einstein's tenets, according to the observer with rest-mass M_o its mass is given by

m = mo √(1 - v2/c2)

and its volume is given by

Einstein maintains that these relations are reciprocal. So the density D of the moving mass, according to the observer of rest-mass M_o, is

D = mo Lo3 (1 - v2/c2)

which is allegedly infinite when v = c (but is then actually undefined): but this is forbidden by Special Relativity since no material object can travel at the speed of light in vacuo (or equivalently, because it requires an infinite energy, which is impossible). So infinite densities are forbidden by Special Relativity. Now the supposed 'point-mass' singularity of the alleged black hole, according to the cosmologists, has a finite mass and a zero volume, so that it is infinitely dense. So if General Relativity permits point-mass singularities it does so in violation of Special Relativity. Yet General Relativity is supposed to be a generalisation of Special Relativity. It cannot therefore violate Special Relativity. So if General Relativity is to be consistent with Special Relativity, it cannot permit point-masses, howsoever they are alleged to be formed. So the point-mass singularity of the alleged black hole is forbidden by the Theory of Relativity, and so black holes are again forbidden by the Theory of Relativity. Furthermore, the Theory of Relativity forbids point charges since there can be no charge without mass.

It should also be noted that the signatures of the alleged black hole are (1) an infinitely dense singularity (point-mass), and (2) an event horizon. Almost daily the astronomers and astrophysical scientists claim discovery of yet another black hole here or there. However, if you ask any of them for the coordinates of just one infinitely dense singularity (point-mass) or the coordinates of just one event horizon, for any of the many hundreds of black holes they allege to have found, you will get no set of coordinates, because nobody has ever found the tell-tale signatures of a black hole - no singularity and no event horizon. Hence, nobody has ever found a black hole. The claims for black holes being found are patently false.

Before one can talk of relativistic binary systems it must first be proved that the two-body system is theoretically well-defined by General Relativity. This can be done in only two ways: (a) Derivation of an exact solution to Einstein's field equations for the two-body configuration of matter; or (b) Proof of an existence theorem. There are no known solutions to Einstein's field equations for the interaction of two (or more) masses, so option (a) has never been fulfilled. No existence theorem has ever been proved, by which Einstein's field equations even admit of latent solutions for such configurations of matter, and so option (b) has never been fulfilled. The so-called 'Schwarzschild' black hole is allegedly obtained from eq. (2) above, a line-element satisfying R_μν = 0. Assuming for the sake of argument that black holes are predicted by General Relativity, since R_μν = 0 is a statement that there is no matter in the Universe, one cannot simply insert a second black hole into the spacetime of R_μν = 0 of a given black hole so that the resulting two black holes (each obtained separately from R_μν = 0) mutually interact in a mutual spacetime that by definition contains no matter! One cannot simply assert, as the black holers do, by a false analogy with Newton's theory, that two black holes can be components of binary systems, collide or merge, because the Principle of Superposition, valid in Newton's theory, is invalid in Einstein's theory, owing to the latter's non-linear character. General Relativity has to date been unable to account for the simple experimental fact that suspended two bodies, initially held fixed, will approach one another upon release. So all talk of black hole interactions is meaningless.

The cosmologists claim, in relation to eq. (2), that since the Riemann tensor scalar curvature invariant (the Kretschmann scalar) is finite at their r = 2m, the latter is a 'coordinate singularity' or 'removable singularity'. This argument is spurious. First, the cosmologists have never proved that Einstein's theory requires a singularity where the Kretschmann scalar is unbounded - they just assert, erroneously, that it is necessary. Second, the Kretschmann scalar is not an independent curvature invariant. Although the Kretshmann scalar depends upon all the components of the metric tensor, all the components of the metric tensor are functions of the Gaussian curvature of the spherically symmetric geodesic surface in the spatial section, owing to the form of the line-element. After all, at any point in a spatial section of the spacetime described by eq. (2), there is a spherically symmetric geodesic surface containing that point, and so there is a Gaussian curvature at that point, in that surface. Third, Einstein's gravitational field is manifest in the curvature of spacetime, a curvature induced by the presence of matter. It is therefore to be expected that the Gaussian curvature of a spherically symmetric geodesic surface in the spatial section of the related metric is also a function of the mass allegedly present, and this is indeed the case, but the black holers are entirely ignorant of this fact too. Eq. (5) gives the modification, imposed by the intrinsic geometry of the line-element and the required boundary conditions specified by Einstein, in consequence of which the Kretschmann scalar is constrained by the intrinsic Gaussian curvature of the spherically symmetric surface in the spatial section. Recall that the Kretschmann scalar, f is

Using eq. (5) gives

f = 12α2K3 = 12α2 Rc6 = 12α2 (|r - ro|n + αn)6/n = 12α2 (Dn + αn)6/n

then

f (ro) = 12 α4

which corresponds to R_p(r_o) = 0 and K = 1/α² (so R_c(r_o) = α). Thus, as the parametric distance D between any two arbitrary points in Minkowski space approaches zero, the corresponding geodesic radial distance from the point at the centre of spherical symmetry of the spatial section of the gravitational field approaches zero and the associated Gaussian curvature approaches 1/α² and the Riemann tensor scalar curvature invariant approaches 12/α⁴, irrespective of the values of r_o and n, and so must also apply to eq. (2), which is a particular case of eq. (5).

Doughty has shown that the geodesic radial acceleration of a point in a manifold described by a line-element with the form of eq. (2) is given by,

a = (-g11)½(-g11)|g00,1| 2g00

Using eq. (5) once again, the acceleration is

a = α Rc3/2(Rc - α)½

and so at R_p(r_o) = 0, R_c(r_o) = α so that the acceleration is divergent. Since the intrinsic Gaussian curvature K = 1/α² at R_p(r_o) = 0, there is no possibility for R_c < α, as eq. (5) shows. Now according to eq. (2), for which r_o = α = 2m, n = 1, r > r_o, the acceleration is

a = α r3/2(r - 2m)½

which is divergent as r -> 2m. But the cosmologists' unproved (and invalid) assumption that r in eq. (2) can go down to zero means that there is a divergent acceleration as r -> 2m where, according to the cosmologists, there is no matter! However, r cannot take values less than r = r_o = 2m in eq. (2), as eqs. (5) and (13) show, by virture of the nature of the Gaussian curvature associated with the spacetime metric and the intrinsic geometry of the line-element.

The cosmologists have admitted that if 0 < r < 2m in their metric eq. (2) above, the roles of t and r are interchanged (see for example, section 1.2 of Bruhn's article). Both Droste and Brillouin also noted this in their papers on the subject, in 1916 and 1923 respectively. For eq. (2), when 2m < r the signature of eq. (2) is (+,–,–,–). But if 0 < r < 2m in eq. (2), then

g00 = (1 - 2m r ) is negative, and

g11 = -(1 - 2m r )-1 is positive.

So the signature of eq. (2) changes to (–,+,–,–). Thus the roles of t and r are interchanged, i.e. there is an interchange of time-like and space-like terms. To amplify this, set t = r* and r = r*, so that for 0 < r < 2m, eq. (2) becomes,

which has the signature (–,+,–,–). But this is now a time-dependent metric since all the components of the metric tensor are functions of the time-like r*, and so this metric bears no relationship to the original time-independent problem to be solved. In other words, this metric is a non-static solution to a static problem:- contra-hype! Thus, in eq. (2), 0 ≤ r < 2m is meaningless, as eqs. (5) and (13) show. Both Droste and Brillouin drew particular attention to this consequence in their respective papers, cited herein.

Bruhn, 't Hooft, MacCallum, Krasinski and Kerr, as are all the black holers and big bangers, are also ignorant of the fact that Einstein's pseudo-tensor cannot be used for anything because it implies the existence of a 1^st-order intrinsic differential invariant, i.e. an invariant that depends only upon the components of the metric tensor and their 1^st-derivatives, rendering it therefore a meaningless concoction of mathematical symbols, because the pure mathematicians G. Ricci-Curbsatro and T. Levi-Civita proved, in 1900, that such invariants do not exist! When confronted with this fact, 't Hooft, the Editorial Board of the IJTP, and other black holers, again maintained silence. Here is the proof (due to the mathematician T. Levi-Civita)) that Einstein's pseudo-tensor is just plain nonsense.

Einstein's pseudo-tensor, √(-g) t^μ_ν, is defined by

√(-g) tμν = ½(δμν L - ∂L ∂gσρ,μ gσρ,ν)

where L is given by

Contracting eq.(14) produces a linear invariant, thus

√(-g) tμμ = ½(δμμ L - ∂L ∂gσρ,μ gσρ,μ)

Since L is, according to eq.(15), quadratic and homogeneous with respect to the Riemann-Christoffel symbols and therefore also with respect to the g^σρ_,μ one can apply Euler's theorem to obtain,

∂L ∂gσρ,μ gσρ,μ = 2L

Substituting (17) into (16) yields the linear invariant at L. This is a 1^st-order intrinsic differential invariant, which Ricci and Levi-Civita proved, in 1900, do not exist! Consequently, Einstein's pseudo-tensor and everything developed using it, are entirely meaningless - just plain nonsense.

MacCallum tried to argue that my analysis and that of Abrams before me must be wrong because it results that the point in the gravitational manifold at the centre of spherical symmetry of the gravitational field has a positive and finite surface area. However, he failed to see that the volume of the said point is precisely zero, as the triple integral for volume on eq. (5) shows. This geometrical oddity is an inevitable consequence of the common form of eqs. (2), (3), (4) and (5) and the associated Gaussian curvature. That it results in such an oddity should not be so surprising, bearing in mind that the indefinite metric of Einstein's theory admits of other geometrical oddities, such as null vectors, i.e. non-zero vectors of zero length (or equivalently, non-zero vectors that are orthogonal to themselves), to which MacCallum and the cosmologists at large express no objections. Apparently they think that the curvature of spacetime must occur on their self-serving terms rather than on the terms required by geometry.

Recall that Ric = R_μν = 0 describes the field conditions for the Schwarzschild class of solutions. Ric = 0 attests to the absurdity of the claims for black hole interactions, as explained above (assuming for the sake of argument that General Relativity predicts black holes, which it does not). Now concerning his 'Principle of Equivalence' Einstein says (see his book, 'The Meaning of Relativity'),

"Let now K be an inertial system. Masses which are sufficiently far from each other and from other bodies are then, with respect to K, free from acceleration. We shall also refer these masses to a system of co-ordinates K', uniformly accelerated with respect to K. Relatively to K' all the masses have equal and parallel accelerations; with respect to K' they behave just as if a gravitational field were present and K' were unaccelerated. Overlooking for the present the question as to the 'cause' of such a gravitational field, which will occupy us later, there is nothing to prevent our conceiving this gravitational field as real, that is, the conception that K' is 'at rest' and a gravitational field is present we may consider as equivalent to the conception that only K is an 'allowable' system of co-ordinates and no gravitational field is present. The assumption of the complete physical equivalence of the systems of coordinates, K and K', we call the 'principle of equivalence'; this principle is evidently intimately connected with the law of the equality between the inert and the gravitational mass, and signifies an extension of the principle of relativity to co-ordinate systems which are in non-uniform motion relatively to each other. In fact, through this conception we arrive at the unity of the nature of inertia and gravitation."

...

"Stated more exactly, there are finite regions, where, with respect to a suitably chosen space of reference, material particles move freely without acceleration, and in which the laws of special relativity, which have been developed above, hold with remarkable accuracy."

Notice that Einstein talks about the presence of more than one body, by which his 'Principle of Equivalence' manifests (neither the 'Principle of Equivalence' nor the laws of Special Relativity can manifest in a spacetime that is "empty", devoid of matter, by definition). Now Ric = 0 is a statement that there is no matter whatsoever in the Universe. Consequently, Einstein's 'Principle of Equivalence' cannot be satisfied in the alleged spacetime manifold of Ric = 0. The laws of Special Relativity also cannot manifest in the manifold for Ric = 0 because there is no matter present by definition. According to Einstein, the curvature of spacetime, by which the gravitational field manifests, is due to the presence of matter, and the energy-momentum tensor is the mathematical object in his field equations which describes the configuration of the matter. If the energy-momentum tensor is set to zero, as is the case for Ric = 0, there is no causative matter present by which the curvature of spacetime can be induced, nothwithstanding the claims by Einstein and the black holers that Ric = 0 describes the field "outside" a body in an otherwise "empty" universe. Furthermore, matter and radiation cannot just be introduced into the manifold for Ric = 0 post hoc because doing so contradicts Ric = 0. Nonetheless, cosmologists do just that (see any of their books and papers). They begin with Ric = 0 (no matter present by definition, but they still claim that a material source is nonetheless present in the universe of Ric = 0, but no other masses or electromagnetic radiation) and then introduce into the manifold for Ric = 0, via their eq. (2) for instance, post hoc, the alleged source of the field m, a material observer, his material measuring instruments, and electromagnetic radiation, all allegedly locally satisfying the laws of Special Relativity (with inertial systems), in direction violation of Ric = 0. Moreover, according to the cosmologists, their observer falls towards their infinitely dense point-mass singularity, from 'infinity'. In so doing their material observer and his accoutrements can acquire any speed up to but not including that of light in vacuo. This means that the mass of the observer, and his measuring instruments, relative to the alleged source of the gravitational field for Ric = 0, are subject to the mass dilation of Special Relativity and so can become arbitrarily large (but not infinitely large) at any instant, in violation of Ric = 0 for the manifold in which the observer allegedly falls. Furthermore, any other masses defining the alleged 'freely falling' inertial frame of the material observer are subject to the same effects, as are any pieces of matter located within that 'freely falling' inertial frame by which the observer can realise the laws of Special Relativity therein, including mass dilation, again in violation of Ric = 0. Now consider the miraculous 'test-particle' of which the cosmologists are so fond. If the 'test particle' is small, it still violates Ric = 0 as it is still subject to the laws of Special Relativity as it 'falls freely', and so its mass can become arbitrarily large at any instant, again in violation of Ric = 0. If the 'test particle' has no mass, no momentum, or any other sources of energy (so it is effectively just a moving point), consistent with Ric = 0, then neither the laws of Special Relativity nor the 'Principle of Equivalence' can manifest, and so Ric = 0 violates the 'Principle of Equivalence'. Thus, whether a material observer is introduced into the manifold for Ric = 0 or a 'test particle' is introduced, a contradiction is immediately introduced. So Ric = 0 does not describe Einstein's gravitational field owing to violation of Einstein's 'Principle of Equivalence' (see Einstein's remarks above); which is not surprising really, since according to Einstein himself his Theory of General Relativity requires that matter be present for a gravitational field to be present and that the causative matter is described by the energy-momentum tensor.

Now recall that Einstein's field equations are:

where G_μν is Einstein's tensor, T_μν the energy-momentum tensor and κ a constant. In consequence of the inadmissibility of Ric = 0, Einstein's field equations must be written in the form first proposed by H. A. Lorentz (in 1916) and independently by T. Levi-Civita (in 1917),

Gμν κ + Tμν = 0

where G_μν/κ are the components of a gravitational energy tensor. This means that Einstein's tensor and the energy-momentum tensor must vanish identically; the total energy is always zero; there is no localisation of gravitational energy (i.e. no Einstein gravitational waves). The LIGO project and its international counterparts, AIGO in Australia and VIRGO in Europe, are giant white elephants, destined to detect nothing.

The field equations

where λ is the so-called 'cosmological constant', are physically meaningless because the energy-momentum tensor is still zero, so that there is no matter present. This expression has been claimed to define empty spacetimes which are curved by themselves, that is, effectively, the existence of gravitational fields in the total absence of matter and energy, which is nonsense (recall that according to Einstein his theory is based upon the idea that the gravitational field manifests as the curvature of spacetime owing to the presence of matter). Not only is eq. (20) inconsistent with the very foundations of Einstein's General Theory of Relativity (see his own remarks above), there is not a single shred of physical evidence that even remotely suggests that a gravitational field (in General Relativity the curvature of spacetime) can exist in the absence of matter. It should also be noted that the cosmologists allege that Ric = 0 contains a material source (not accounted for by any energy-momentum tensor) of a gravitational field in an otherwise empty universe. There is no meaning to the gravitational field of a single object. The gravitational field manifests as an interaction between two or more bodies, which is not described by Ric = 0. Einstein's gravitational field is no different to Newton's in this regard, and it too cannot be detected except by means of a priori interactions between masses and/or radiation (see eqs. (18) and (19) above). Newton's theory is based upon the a priori interaction of two or more bodies and his law of gravitational is couched in terms of two interacting masses in a space in which any number of masses can exist, a priori. Furthermore, although the black holers claim that a source of a gravitational field is present for Ric = 0, they do not claim that such a source is present in relation to eq. (20) (for example, de Sitter's empty universe), even though the energy-momentum tensor is also zero in eq. (20) (i.e. T_μν = 0). thus the cosmologists assert that matter is both present and absent by the very same mathematical constraint! So the black holers allege the presence of matter when it suits them. The fact is, according to Einstein's theory, Ric = 0 excludes all matter by definition.

Now, most importantly, owing to the inevitable form of Einstein's field equations, eq. (19), his General Theory of Relativity violates the usual and experimentally well established conservation of energy and momentum for a closed system. There is no experimental evidence that the usual conservation of energy and momentum is invalid, so experiment does not support Einstein. Thus General Relativity is invalid owing to its violation of the usual conservation of energy and momentum. Consequently, not only are black holes therefore nonsense, so is the big bang cosmology and all its trappings.

Concerning my challenge to the black holers and big bangers, on or about 31 October 2007 F. W. Hehl scribbled me the following insipid email:

"Dear Simplifier,

Is this a substitute for your non-existent Ph.D. thesis?

Friedrich W. Hehl"

I remark that the ignoble Herr Hehl was also invited to provide a proof that the quantity 'r' in eq. (2) is the radius. He ignored the invitaton.

Here is the response of Messrs. Taylor and Bertschinger to my exposure of the fatal errors in the arguments they expound in their book 'Exploring Black Holes':

They then stated that they would not enter into any further discussion and would publish their book anyway. Here is the correspondence from Taylor.

On 20^th February 2008 I sent this paper to the International Journal of Theoretical Physics, requesting publication. On 21^st February 2008 I sent them this paper. Both papers are very short and very simple, but nonetheless fatal to the black holers and big bangers. In two emails dated 14^th April 2008 I was told by the Editorial Board;

"Dear Mr. Stephen J. Crothers,

I have received the decision from the Editor on your manuscript, IJTP1960 "Point-Mass Singularities, Energy and the Two-Body Problem in Einstein's Gravitational Field"

We thank you for your kind offer to let us publish your manuscript, but regret to inform you that we have decided not to accept your offer. The paper did not undergo technical review and is not being declined for any technical error. We wish you every success in finding an alternative place of publication.

With best regards,

International Journal of Theoretical Physics

H. Saller

Editor in Chief"

"Dear Mr. Stephen J. Crothers,

I have received the decision from the Editor on your manuscript, IJTP1962 "Concerning Radii in Einstein's Gravitational Field"

We thank you for your kind offer to let us publish your manuscript, but regret to inform you that we have decided not to accept your offer. The paper did not undergo technical review and is not being declined for any technical error. We wish you every success in finding an alternative place of publication.

With best regards,

International Journal of Theoretical Physics

H. Saller

Editor in Chief"

Here is my reply,

"Dear Prof. Saller,

Please advise as to why my paper has been declined.

Yours faithfully,

Stephen J. Crothers."

So despite the Editorial Board of the IJTP having found no technical errors in my two papers (they must have read them to know what's in them) they refused to publish them, refused to send them to the nominated referees (for whom they called in the first place), refused to discuss the contents of the papers, and failed to reply to my request for a reason for their rejection of my papers. If one examines the list of people on the Editorial Board of the IJTP one notices that there are a number of "supermassive" black holers and big bangers there - res ipsa loquitur. Here is the correspondence.

Now Bruhn,'t Hooft, MacCallum, Krasinski, Kerr and various other black holers and big bangers have not only taken umbrage at my work but also at my style of exposition. Apparently they think me offensive in my manner and maintain that I should let them walk all over me and insult me as they please, without any retaliation. An ardent black holer, claiming to be a qualified scientist, recently called me, in writing, in a Web physics forum, "a fucking moron", and "a notorious crank". Other black holers, including some professors of physics (e.g. Krasinski), have called me other, but not too dissimilar, things, and R. Kerr is not averse to referring to me with four-letter words. Not very gentlemanly, and hardly scientific, but the cosmologists evidently think this scientific method, at least when dealing with people who question their arguments or expose their mistakes. Krasinski even told a third party that I must not be believed because I am a "maniac" who infected his computer with viruses I have hidden away in the code for my webpages, to wreak revenge upon cosmologists.

Stephen J. Crothers

My email

Home Page

Page established: 30 March 2008