My Malicious, Gormless Critics

A number of quite malicious proponents of black holes and Big Bang Cosmology, adducing no arguments of their own devise, have resorted to merely citing the following equally feckless quintet, on a number of blogs and other websites, in their unreasonable protestations to my proofs that Black Hole universes and Big Bang universes are nonsense:

1. Gerardus 't Hooft, Nobel Laureate (physics)

2. William Clinger

3. Jason J. Sharples

4. Christian Corda

5. G. W. Bruhn

I have dealt thoroughly with the quintet elsewhere:

1. 't Hooft,
2. Sharples (a), Sharples (b), Sharples (c)
3. Bruhn
4. Corda (a), Corda (b)
5. Clinger

A common mathematical issue of the 'quintet' is the alleged 'extension' of Droste's solution to Hilbert's solution. It is from the latter that the black hole was first conjured. Cosmologists always and incorrectly call Hilbert's solution "Schwarzschild's solution". However, it is an irrefutable fact that Hilbert's solution is not Schwarzschild's solution, which can be easily verified by reading Schwarzschild's original paper and comparing it to Hilbert's scribblings. Droste's solution is equivalent to Schwarzschild's solution but Hilbert's 'solution' is not.

The equivalence of the Schwarzschild and Droste solutions is easily established. Here they are (in both cases the speed of light in vacuum, c, is set to unity):

The constant α is positive but otherwise indeterminable. Note that Droste's r = α corresponds to Schwarzschild's r = 0. In both cases ds² is then undefined (i.e. 'singular') because the coefficient in the second term on the right side produces -1/0. Contrary to the practice of cosmologists (who claim that 1/0 = ∞), division by zero is undefined. Compare now to Hilbert's 'solution' (here c = 1 and G = 1 in the 'Schwarzschild radius' r_s = 2Gm/c²):

Note that Hilbert's r = r_s = 2m corresponds to Droste's r = α and Schwarzschild's r = 0, but that neither Schwarzschild's nor Droste's solution possess values corresponding to Hilbert's 0 ≤ r < 2m. Consequently Hilbert's solution is not equivalent to Schwarzschild's and Droste's. Also note that according to Hilbert, Einstein, and the cosmologists, the constant m in Hilbert's solution denotes the mass that is the source of a gravitational field allegedly produced by it.

The solutions obtained by Schwarzschild and Droste are not only equivalent, they are elements of an infinite equivalence class, i.e. an infinite set of equivalent solutions. All elements of this infinite equivalence class describe the very same geometry, so they are effectively the same solution. Just as something can be described in different words, so too the same mathematical solution can be described in different symbols. That being so, if any element of this equivalence class is extendible in the fashion of Hilbert's solution, then all must be extendible. Conversely, if any element of the equivalence class is not extendible then none are extendible. What then is the ground-form or generator of the equivalence class? This was adduced in my very first paper on the subject (in 2005), yet none of my critics, it seems, have noticed it. So here it is again;

Here the constant r_o is any real number and the constant n is any positive real number (take your pick). Note that R_c is defined for all values of r and all values of n, and that R_c(r_o) = α for all values of r_o and all values of n. Similarly, ds² is 'singular' only when r = r_o. If r_o = 0, n = 3, r ≥ r_o, then Schwarzschild's solution is obtained. If r_o = α, n = 1, r ≥ r_o, then Droste's solution is obtained. It is clear from the metric ground-form that no (equivalent) solution generated by it can be extended in the fashion of Hilbert, to thereby produce a black hole. This is amplifed by taking r_o = 0 and n = 2, to yield,

This metric is defined for all values of r except r = r_o = 0. It can't be extended to -α² ≤ r² to produce a black hole, because r² can never have values less than 0, and hence R_c can never have values less than α. Thus, on account of equivalence, no element of the infinite equivalence class can be extended to produce a black hole. Hence, Droste's solution cannot be extended to Hilbert's 'solution' and so there is no possibility of a black hole 'solution'. Similarly, Schwarzschild's solution cannot be extended. Consequently, there is no black hole universe. All other black hole universes rely upon Hilbert's, and so they are all false. The black hole requires, in the specific example above, that -α² ≤ r², which is a violation of the rules of pure mathematics. In general, the mathematical theory of black holes requires that -αⁿ ≤ |r - r_o|ⁿ. The mathematical theory of black holes violates the rules of pure mathematics. Consequently, it is certainly false.

A Few Other Closely Related Issues

Einstein's field equations are:

λ is the 'cosmological constant'. T_μν is the energy-momentum tensor that describes the material sources of Einstein's gravitational field. The left side of the equation gives spacetime geometry, which is curved due to the presence of material sources, and this spacetime curvature is Einstein's gravitational field. According to Einstein, matter must be present to produce his gravitational field, i.e. to induce the curvature of his spacetime. According to Einstein and his followers, if λ = 0 and T_μν = 0, the field equations reduce to,

Einstein and his followers assert that R_μν = 0 describes his gravitational field 'outside a body such as a star'. However, this reasoning is circular, and therefore false, since all material sources are removed mathematically by setting T_μν = 0, then a material source is immediately reinstated with the words 'outside a body such as a star'. Since T_μν = 0, there are no material sources present to produce any gravitational field. Therefore, R_μν = 0 has no physical meaning. But the black hole was conjured from Hilbert's 'solution' to R_μν = 0. Since R_μν = 0 is physically meaningless so too is Hilbert's solution for it, as are the solutions by Schwarzschild and Droste. Therefore, the black hole is a fantasy.

That R_μν = 0 contains no matter whatsoever, and hence cannot lead to a black hole at all, is reaffirmed by the case, λ ≠ 0, T_μν = 0, in which case Einstein's field equations become,

The solution for these equations is de Sitter's empty universe, which is empty because it contains no material sources (T_μν = 0), even though the solution has a non-zero curvature. Matter is the source of Einstein's gravitational field, and, according to Einstein, matter is everything except his gravitational field. Without material sources no gravitational field can be produced. So 'spacetime curvature' alone, without material sources to induce it, does not produce Einstein's 'gravitational field'. By virtue of R_μν = 0 and R_μν = λg_μν, Einstein and his followers assert that material sources are both present and absent by the very same mathematical constraint (T_μν = 0); which is impossible. Since de Sitter's empty universe contains no material sources (it's empty), R_μν = 0 also contains no material sources for the very same reason (T_μν = 0), and so there is no black hole, and the Big Bang creationism is also false, since the latter is inextricably intertwined with black holes (in their billions!).

The quantity r in Hilbert's solution is not even a distance let alone the radius therein. Nonetheless the cosmologists always treat it as the radius. This is most evident in the so-called 'Schwarzschild radius' of their black holes, and even of stars and planets. According to the cosmologists their 'Schwarzschild radius' r_s = 2Gm/c² is the 'radius' of the event horizon of their black hole, which, they say, is centred at Hilbert's r = 0 (their 'singularity'). They also routinely assert that the 'Schwarzschild radius' of the Sun and of the Earth lie deep within them, and that if the Sun became a black hole it would have a 'Schwarzschild radius' of ~3km. What then is the true geometric identity of r in Hilbert's 'solution'? It is easily proven that it is the inverse square root of the Gaussian curvature of the spherically symmetric surface contained in the spatial section of Hilbert's metric. Hence, the 'Schwarzschild radius' is not the radius of anything in Hilbert's solution. What is the spatial section of Hilbert's metric? It's everything that does not contain dt. In this regard it is also important to note that the intrinsic geometry of a surface is competely independent of any higher dimensional space in which it might be embedded. How many dimensions does a surface possess? Two.

According to the cosmologists their black hole has a finite mass. This mass is inserted post hoc into Hilbert's 'solution', by insinuating the Newtonian expression for escape speed, in order to satisfy the false assertion that R_μν = 0 contains a material source, 'such as a star'. Moreover, Newton's expression for escape speed is an implicit 2-body relation (one body escapes from another body), and so it cannot rightly appear in what is alleged to be a solution for a 1-body problem, such as a star or black hole in accordance with Einstein's R_μν = 0. Rearranging the equation for the so-called 'Schwarzschild radius' gives,

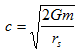
This is immediately recognised as the Newtonian expression for escape speed. It is from this equation that the cosmologists obtain the speed of light for the 'escape speed' at their black hole 'event horizon' (i.e. at their 'Schwarzschild radius'). No cosmologist even understands the meaning of 'escape velocity'. On the one hand, according to the cosmologists, their black hole has an escape velocity. At their black hole 'event horizon' they assert that the escape speed is the speed of light. On the other hand they also assert that nothing can even leave their event horizon. The event horizon is a one-way membrane: things can go into the black hole but nothing can emerge. Light, they say, hovers forever at the 'event horizon' when trying to 'escape' from there. However, escape speed does not mean that nothing can leave, only that physical things cannot escape if they do not achieve the escape speed. Thus, on the other hand the cosmologists assert that their event horizon has no escape speed, since nothing can even leave it. So their black hole has the schizophrenic properties of having and not having an escape speed simultaneously at the same place (at the 'event horizon'). But nothing can have and not have an escape velocity simultaneously at the same place. Furthermore, since light travels at the speed of light, and the escape speed at the event horizon is the speed of light, then, by definition of escape speed, light must escape! But not according to the cosmologists; light hovers forever at their event horizon.

According to the cosmologists, the finite mass of their black hole is concentrated at the 'physical singularity' of their black hole (i.e. at Hilbert's r = 0), where, they say, volume is zero, density is infinite, and spacetime is infinitely curved. There are forces in General Relativity, but gravity is not one of them, because it is spacetime curvature. Thus, according to the cosmologists, at their 'physical singularity', a finite mass produces infinite gravity! However, no finite mass has zero volume, infinite density, infinite gravity, anywhere. Once again, the theory of black holes flase.

All this and more has been explained in detail in my papers and video recordings.

Stephen J. Crothers

Home Page

My email address: thenarmis@yahoo.com

Page established: 9^th June 2015